Mivel a legtöbb esetben PCM hangfájlokkal dolgozunk, és a sorozat eddigi részeiben is ezt használtuk, ezért most is csak a PCM formátumról lesz szó.
Digitálisan tárolt hang ábrázolása
A hanghullám előre-hátra irányban mozgatja a mikrofon membránját, és a hangszóró is ilyen mozgással adja vissza azt, ezeket az elmozdulásokat pedig egy nulla, vagyis nyugalmi alaphelyzethez képest értjük. Ez az alapállapot a levegőben mindig jelenlévő atmoszferikus nyomás (a mellékelt ábrán P atm), ami egyben a hanghullámot leíró függvényünk 0 értéke is. Nem véletlen tehát, hogy a nyugalmi állapot az analóg rendszerekben szintén 0 V feszültségnek felel meg. A levegőrészecskék mozgása előre-hátra irányban, ehhez a nulla volthoz képest pozitív és negatív feszültséget indukál, vagyis váltakozó áramot állít elő (lásd a lenti ábrán). De vajon mi a helyzet a digitalizálás után? Fontos tudni, hogy a digitalizáció során nem magát az éppen mért feszültségértéket raktározzuk el (pl. +5 V), hanem az aktuális feszültségérték és a referencia-feszültségérték viszonyát. Vagyis például a legmagasabb ábrázolható minta érték nem egy adott feszültséget jelent, hanem a hullámforma csúcsát. Ezt később aztán olyan feszültséggé tudjuk visszaalakítani, amilyenné szeretnénk, vagyis amit a DA konverter referencia feszültségnek használ. Adott tehát a kérdés, hogy digitálisan tárolt hang esetében vajon van-e egyáltalán olyan, hogy plusz és mínusz érték, és ha igen, hogyan tároljuk azt? Bár 4 különböző kódolás terjedt el, alapvetően csak két fő lehetőség közül választhatunk.
Előjel nélküli ábrázolás
Mivel digitalizáláskor ismerjük a használt referencia feszültséget, és ehhez hasonlítjuk a beérkező feszültségeket, így ismerjük a lehető legalacsonyabb (mínusz volt) és legmagasabb (plusz volt) értékeket is. Ha a legalacsonyabb feszültségértéket (mínusz max.) feleltetjük meg a digitálisan tárolható legalacsonyabb értéknek (vagyis nullának), és a legmagasabb értéket (plusz max.) a digitálisan tárolható legmagasabb értéknek, akkor úgynevezett nem előjelezett, angolul unsigned formátumban tároljuk az adatokat (lásd a mellékelt ábrán, vörös színnel jelölve). Vagyis itt csak nullát és pozitív egész számokat tárolhatunk, negatívat nem. Ez persze nem jelenti azt, hogy ebből ne tudnánk visszaállítani az eredeti váltakozó áramú analóg hullámformát. 16 bites audió esetében az ábrázolható decimális tartomány 0-65535 között helyezkedik el, ami azt jelenti, hogy ennyi feszültségértéket tudunk megkülönböztetni a maximális és minimális referencia érték között.
Előjelezett ábrázolás
Ha azt szeretnénk, hogy a digitálisan tárolt adatok jobban "hasonlítsanak" az eredeti feszültségértékekre, akkor a 0 V értéket a digitálisan ábrázolható számérték közepére helyezzük, és innen ábrázolunk pozitív és negatív irányba. Ebben az esetben úgynevezett előjelezett, angolul signed formátumról van szó, amit 3 különböző kódolással tárolhatunk. A konverterek (AD és DA) általában a bináris ofszet (offset binary), vagyis eltolt bináris ábrázolást használják, ahol a legmagasabb helyiértékű bit (MSB, vagyis a leginkább balra eső bit) jelzi, hogy pozitív vagy negatív számról van-e szó. Ebben az esetben az ábrázolható értékek 16 bites audió esetében −32768-tól +32767-ig tejednek. Egy másik lehetséges kódolási mód az előjel és érték (sign and magnitude), ahol szintén az MSB adja meg, hogy pozitív vagy negatív értékről van-e szó, de ebben a kódolásban a nulla érték lehet pozitív és negatív is, ezért itt egyel kevesebb számot tudunk csak ábrázolni, vagyis "elpazaroltunk" egy bitet. Az ábrázolható értékek ennek megfelelően 16 bites audió esetében −32767-től +32767-ig tejednek.
Az eddig megismert 3 ábrázolási mód fogalmilag egyszerűnek mondható, viszont nehéz hardverre átültetni, mert a tervezőmérnöknek ki kell találnia, hogyan tud megbizonyosodni róla, hogy egy-egy művelet elvégzésekor éppen melyik kódolást választottuk. Ezért létrehoztak egy negyedik kódolási formát is, ami leegyszerűsíti a pozitív és negatív számok megkülönböztetését, és a velük végzett műveletek helyes elvégzését (legalábbis a hardver számára). Ez a kettes komplemens (two's complement), ami nekünk embereknek talán egy kicsit bonyolultabb, de a gépeknek sokkal biztosabb. A lényeg, hogy nulla érték esetén (ami középen helyezkedik el) minden bit 0. Pozitív számok esetén "normál" módon ábrázoljuk az értéket, negatív számok esetén viszont kettő komplemensét alkalmazzuk, ami azt jelenti, hogy "invertálva" írjuk fel a számot. Ahol bináris 0-nak kéne lennie, ott bináris 1-et írunk, és fordítva, majd a konvertálás végén hozzáadunk a számhoz 1-et. Vagyis itt 0-tól visszafelé kezdünk el számolni, tehát -1, esetében az összes bit 1-re lesz állítva, pont ugyanúgy, mintha az autó kilóméter-számlálóját visszafelé kezdenénk el forgatni, így a megjelenő szám 99999, majd 99998... stb lesz. Ebben az esetben az ábrázolható értékek 16 bites audió esetében −32768-tól +32767-ig tejednek, ahol az MSB 0 értéke esetén pozitív, vagy nulla számról van szó, 1 érték esetén pedig negatívról. A pozitív számoknál az átváltás egyszerű, ugyanúgy történik, mint a másik három kódolás esetén, negatív számoknál viszont műveleteket kell végezni a kikódolásra, így ez plusz időbe telik.
Természetesen mindezek magát a tárolható feszültségértéket nem befolyásolják, hiszen minden esetben ugyanúgy felhasználjuk az összes rendelkezésre álló bitet, de hogy az eredeti értéket kapjuk vissza, tudnunk kell, hogy mikor melyik kódolást használtuk. Vegyük észre, hogy a fenti 4 esetben csak egész számokat ábrázolhatunk, amit mondhatunk úgy is, hogy a tizedesjel egy bizonyos ponton rögzített (méghozzá a decimális egyes helyiérték mellett jobbra). Ezért ezeknek az ábrázolásoknak a neve Fixpontos ábrázolás.
Fixpontos és lebegőpontos ábrázolás
A bitekről szóló részből már megtudtuk, hogy magához a hangrögzítéshez és visszajátszáshoz nem csak hogy nincsen szükség 24-nél nagyobb bitmélységre, de nem is tudnánk azt sem digitalizálni, sem lejátszani. Mivel a meglévő hardvereszközök csak a fixpontos ábrázolást ismerik, ebből következik, hogy ilyen célra bőven elegendőek ezek is. Ám mindez sajnos nem mondható el a digitálisan tárolt hang feldolgozásáról.
A számítógépek jelenleg csak kettes számrendszerben képesek működni, vagyis adatokat tárolni, mozgatni és számolni. Ez azt jelenti, hogy bármennyi bitet is használunk az adat ábrázolására, az a hardver szintjén csak egész szám lehet. Az egyszerűség kedvéért vegyünk egy 2 bites példát. Itt ugye az első bit (LSB) tízes számrendszerre váltva lehet 0 vagy 1, a második bit pedig 0 vagy 2. Tehát 2 biten ábrázolhatjuk a következő decimális számokat: 0, 1, 2, 3. Vagyis nem ábrázolhatunk 1,5-öt, vagy 0,3-at. Ez miért probléma?
Képzeljünk el egy egyszerű keverési esetet, amikor a digitálisan rögzített hangot szeretnénk a mixben fele hangerőre csökkenteni. A egyszeri hangmérnök nem is tesz mást, mint lehúzza a DAW keverőjében az adott csatorna faderét. Mi történik ilyenkor a DAW-ban?
A hangerő csökkentése nem más, mint a pillanatnyi feszültségértékek csökkentése. Ez nyilvánvaló, hiszen a halkabb hang a legtöbbször alacsonyabb feszültségértéket is jelent. Ha a jelszintet a felére szeretnénk csökkenteni, akkor a feszültségértéket is a felére kell csökkenteni, vagyis osztani kell kettővel. Pontosan ez is történik, a DAW minden minta értéket eloszt kettővel. Ha csak páros számok szerepelnek a mintákban, nincsen nagy gond, hiszen ezeket kettővel osztva minden esetben egész számot kapunk, ami könnyedén felírható fixpontos ábrázolással. Na de mi van akkor, ha a minta értéke mondjuk 3? Annak a fele 3/2, vagyis 1,5, ami nem egész szám, tehát a fenti rendszerben nem tudjuk ábrázolni. Ahhoz, hogy az eredménynek legalább egy része megmaradjon, kerekítenünk kell. Ebben az esetben vagy 1, vagy 2 lesz a kapott érték, az osztó algoritmus programozása szerint. A művelet során tehát ugyanolyan kerekítési, vagyis kvantálási hiba keletkezik, mint digitalizáláskor, és mint már tudjuk, ez további kvantálási zajhoz és torzításhoz vezet. Mindennek tetejébe, minél több ilyen törtszámot eredményező műveletet végzünk el, annál több és annál nagyobb hibát viszünk bele a hangba, vagyis a hiba folyamatosan erősödik.
Megoldás lehet, ha az egyes értékeket kódolva ábrázoljuk. Ez jelentheti például azt, hogy létrehozunk egy képzeletbeli tizedes jelzőt, amivel elkülönítjük a tizedes számokat az egész számoktól, akárcsak a hétköznapi matematikában. Ezt a tizedespontot a választott bitmélységen ábrázolható számok egy bizonyos pontjára helyezzük el, így már képesek leszünk tizedes értékeket is ábrázolni, viszont ezzel együtt csökken a szám egészének ábrázolására használható bitek száma. Nézzünk egy példát! Maradjuk az előző 2 bites esetnél, ahol most a jobbra eső bit lesz a tizedes jegy. Ebben az esetben ábrázolható számok: 0, 1, 0,1 és 1,1. Nem sok, de több mint a semmi. Persze ha több bitet használunk és több bitet engedünk át a tizedes jegyeknek, akkor még finomabb ábrázolást is elérhetünk, de minden esetben csökken a maximálisan ábrázolható érték. Megoldás lehet persze az is, ha a tizedes jegyeket kódoljuk, például a fenti esetben a jobbra eső bit 1 értéke 0,5-öt jelent. Ilyenkor már ábrázolhatjuk a fél számokat is. Ebben az esetben persze minden művelet elvégzése előtt és után is kódolnunk kell, ami persze extra idő elhasználását jelenti. Ennek a megoldásnak egy további óriási hátránya, hogy csak előre meghatározott számú tizedest tudunk használni. Ez két okból probléma: 1. ha ezekre nincsen szükség, akkor csak feleslegesen foglalják a helyet, 2. ha túl kevés a tizedes, akkor szintén kerekítési problémába ütközünk. Egy másik probléma, hogy a rögzített tizedesek elveszik a helyet a nagy számok ábrázolásától. Vagyis se nagy számokat, se kis számokat nem tudunk korlátlan (vagy legalábbis közel korlátlan) pontossággal ábrázolni.
A probléma megoldására megszületett a lebegőpontos ábrázolás, ami lehetővé teszi, hogy valós számokat ábrázolhassunk véges tárhelyen (a bitek számán), méghozzá széles tartományban. Működése alapjában véve nagyon egyszerű! A lebegőpontosan ábrázolt szám alapvetően két részből áll, egy úgynevezett mantisszából és a kitevőből. Hasonlóval találkozhatunk az úgynevezett tudományos számábrázolásnál is, aminek előnye, hogy viszonylag egyszerűen lehet nagyon kicsi és nagyon nagy számokat egymás mellett ábrázolni. Például 1,2e+50 = 1,2x10^50, vagyis 12 és még ötven darab nulla, ami egyenlő a Földön található atomok számával, vagy 2,6e-23=2,6x10^-23, vagyis 0,0000000000000000000000026, ami egyenlő azzal a távolsággal, amit egy teknős mászik egy másodperc alatt, osztva a galaxisunk átmérőjével. Vagyis ezekben az esetekben az "e" utáni érték mutatja, hogy merre kell eltolni a tizedesvesszőt és hány számjegyet. Tehát a tizedesvessző lebeg. (Figyelem, ez az ábrázolásmód csak tízes számrendszerben érvényes!) Figyeljük meg, hogy maga a pontos érték normalizálva kerül ábrázolásra, ami azt jelenti, hogy mindig csak egy számjegy található a tizedesjel előtt, a tizedesjel valódi helyét pedig a kitevőben jelöljük.
Hasonlóan működik a lebegőpontos ábrázolás a számítógépek esetében is, de itt nem tízes, hanem kettes számrendszerben dolgozunk. Mint látható, ez is egyfajta kódolt szám, és mint ilyen, sajnos többféle változata létezik, attól függően, hogy ki írta a programot. Ebből adódik, hogy néhány esetben a lebegőpontos fájlok nem kompatibilisek az egyes DAW-ok között. A legelterjedtebb szabvány az ANSI/IEEE Std. 754-1985, ami két ábrázolást ír le. Az egyik a 32 bites lebegőpontos, amit normál pontosságúnak neveznek, és a 64 bites lebegőpontos, amit dupla pontosságúnak.
Mint ahogy az ábrán is látszik, a 32 bitet három csoportra osztjuk fel. 0-22 bitek alkotják a mantisszát, 23-30 bitek a kitevőt, és a 31-es bit pedig az előjelet. Ezek együtt határozzák meg a 32 bites lebegőpontos szám valódi értékét (v), mégpedig a következő képlet alapján, ahol (-1)^S (az előjel bit (S)) jelzi, hogy a szám pozitív vagy negatív. Ha a bit 0, akkor a szám pozitív, ha 1, akkor negatív. Az "E" a kitevőben lévő érték, ami 0-255 lehet. Mivel ebből kivonunk 127-et, így lehetővé válik, hogy a 2 hatvány kitevője -127 és +128 között változzon (vagyis az értéket eltolt bináris formában tároljuk). Az egyenletben az "M" jelöli a mantisszát, normalizált tört értékként ábrázolva. Decimális ábrázoláskor például a 2,783 jelentése: 2 + 7/10 + 8/100 + 3 /1000. Bináris alakban az 1.0101 értéke hasonlóan alakul ki, de nem tízes, hanem kettes kitevővel dolgozunk, tehát a valódi érték 1 + 0/2 + 1/4 + 0/8 + 1/16.
A normalizáció ugyanúgy történik meg, mint a tudományos ábrázolásnál, vagyis csak egyetlen nem nulla számjegy maradhat a tizedesjegy előtt (a bal oldalon, amit a kettes számrendszerben kettesjegynek, bináris pontnak hívunk). Mivel a kettes számrendszerben csak egyetlen egy, nem nulla számjegy létezik, az 1, így ezt nem is kell ábrázolnunk, ezzel máris megspóroltunk egy bitet. A mantissza értékét tehát a következő képlettel kapjuk meg: M=1 + m22^-1 + m21^-2 + m20^-3... Ha a 0-22. bitek mind nulla értékűek, akkor a mantissza értéke 1. Ha a 0-22. bitek mind 1 értékűek, akkor a mantissza értéke éppen egy hajszálnyival van 2 alatt, pontosan: 2-2^-23.
Az IEEE 754-1985. szabvány szerint ábrázolható legkisebb és legnagyobb érték azonban nem egyezik az elérhető maximális értékekkel, mert bizonyos számokat speciális jelentéssel ruháztak fel. Ha a mantissza és a kitevő összes bitje 0 értékű, akkor a valódi érték +/-nulla. Ha az összes mantissza bit nulla, és az összes kitevő bit 1, akkor a valódi érték +/-végtelen. Emellett néhány nagyon kicsi normalizálatlan szám is bekerült a csoportba, méghozzá +/- 1,2x10^-38 és +/- 1,4x10^-45 között. Ezek alacsony pontossággal ábrázolt számok, amiket akkor kapunk, ha nem tartjuk be azt a szabályt, hogy a mantissza első számjegye 1 kell hogy legyen. Ezen a három fő csoporton kívül is vannak bizonyos minta szerű kivételek, amiknek nincsen jelentése, egyszerűen csak "nem számoknak", angolul NAN-nak (Not A Number) nevezték el őket. Mindezek figyelembevételével a legnagyobb ábrázolható szám +/- 3,4x10^38, a legkisebb pedig +/- 1,2x10^-38.
A szabvány szerinti dupla pontosságú, 64 bites lebegőpontos ábrázolás ugyanígy működik, de 52 bites mantisszával és 11 bites kitevővel. Gyakorlatilag elmondható, hogy már a 32 bites lebegőpontos ábrázolás alkalmazásával sem nagyon találni olyan feladatot amire az ne lenne elég, az viszont biztos, hogy a 64 bites változat esetében ilyen feladat nem is létezik. Biztos ami biztos alapon azonban a szabványt már most felkészítették a 128 és 256 bites ábrázolásra is.
Lebegőpontos ábrázolás problémái
Sajnos bármilyen hihetetlen pontossággal is képesek a lebegőpontos számok ábrázolni a valódi értékeket, azok minden esetben kerekítésre kerülnek, hiszen a mantissza sem áll végtelen számú bitből (ha abból állna, akkor végtelen sokáig tartana kiszámolni, elmenteni, majd újból előhívni, így végtelen sokat kéne várnunk, amíg csak egyetlen minta is elkészülne). Tehát itt sem szabadultunk meg a konvertereket, és egyéb fixpontos ábrázolást használó szoftvereket sújtó kvantálási hibáktól, egyszerűen csak más formába öntöttük őket.
A lebegőpontos ábrázolás "hibája", hogy valójában nem a felbontást növeli meg, hanem a szám ábrázolásához használt "arányt" változtatja. Ez azt jelenti, hogy egy adott kitevő esetén, az ábrázolható számok között nem végtelenül kicsi a különbség, hanem az ábrázolt számtól, vagyis a kitevőtől függően változik. Általában az ábrázolt szám tízmilliomod részéről beszélhetünk, egészen pontosan 2^-24 és 2^-23 között változik. Ha pl. a kitevő alacsony értékű, akkor csak kis értékű számokat tudunk ábrázolni, viszont az ábrázolható számok között nagyon kicsi lehet a különbség is (lásd a zöld mezőben). Ha viszont az ábrázolni kívánt szám nagy, akkor a számmal együtt az egyes számok közötti különbség is megnő, vagyis egy bizonyos szempontból kevésbé részletes ábrázolás történik (vörös mezőben).
A kerekítési hibák mértéke tehát attól függ, hogy éppen mekkora számmal dolgozunk. Ha nagy számokkal, akkor az abszolút eltérés nagy lesz, ha kicsikkel, akkor kicsi. A relatív eltérés persze azonos marad, de kérdés persze, hogy például kicsi számok esetén megengedhető-e az a kis eltérés is? Ilyen pl. az 1,1, ami pont két lebegőpontosan ábrázolható szám közé esik: 1.0999999046 és 1.1000000238. Mint látható, az eltérés nem nagy, persze kérdés, hogy mihez képest...
Hogy magunk is meggyőződhessünk a lebegőpontos "pontatlanságról", végezzünk el két próbát. Most nem a DAW-ban, hanem egy online BASIC nyelvet használó program-futtató környezetben fogunk dolgozni, amit ide kattintva érhetünk el. Megnyitás után töröljünk mindent a "Source Code" mezőből, és másoljuk be a következő pár sort (CTRL+C és CTRL+V).
100 'Lebegőpontos ciklus vezérlés
110 FOR X = 0 TO 10 STEP 0.01
120 PRINT X
130 NEXT X
A program első sorában egy úgynevezett ciklust hozunk létre, ami 0-tól 10-ig növeli X értékét, méghozzá úgy, hogy minden újabb ciklusban 0,01-et ad X aktuális értékéhez. A 0,01 egy tört szám, vagyis lebegőpontosan kell ábrázolni, tehát a vele végzett műveletek is lebegőpontosan mennek végbe! A következő sorban kiíratjuk X aktuális értékét, majd a 130-as sorban visszaugrunk a 110-es sorra, és a ciklus újból indul, amíg X értéke el nem éri a 10-et.
Mit kéne látnunk, ha majd elindítjuk a programot? Szerintem ez nagyon egyszerű, és gondolom az olvasók is kitalálták már, egy számsort kell hogy kapjunk, pontosan olyat, mint ami a baloldali ábrán látható.
Indítsuk is el a kis programunkat az "Execute" gombra kattintva, és nézzük, mint kapunk!
Mint látható, a lebegőpontos ábrázolás miatt bekövetkező kerekítési hibák bizony eléggé eltérő eredményt adnak ahhoz képest, mint amit matematikailag várnánk. A legmeglepőbb, hogy a ciklus el sem érte a 10-et mielőtt leállt volna. Ezt az összeadódó kerekítési hibáknak köszönhetjük, ugyanis ezeknek köszönhetően X az utolsó ciklus előtt 10.000133-as értéket ért el, ami nagyobb mint 10, ezért a program még az előtt leállt, hogy kiírhatta volna a 10-et. Ez a befejezetlen ciklus egy jellegzetes hiba a számítógépes programokban.
Ha 32 bites lebegőpontos ábrázolásról beszélünk, akkor amíg 24 biten is ábrázolható az adott szám (+/- 2^24, vagyis elfér a mantisszában), és ráadásul egész is, nincsen probléma, ugyanis ezek között a számok között a különbség mindig 1. Az így ábrázolható számok esetében tehát a kerekítés nem ad hibát. (Ha végig gondoljuk mindezt, akkor eltöprenghetünk azon, hogy vajon érdemes-e a 24 bites fixpontosan digitalizált (tehát csak egész számokat tartalmazó hangunkat) lebegőpontossá alakítva feldolgozni...) Ha viszont ennél nagyobb számokról van szó, amit már csak lebegőpontosan tudunk ábrázolni, akkor a különbség az egyes számok között változóvá válik, ezért a számítások elvégzése után végzett kerekítések alkalmával egyes számok kimaradhatnak.
Denormalizációs hiba (denormal)
Régebben a CPU-nak nem csak a program futtatását, de a lebegőpontos számokkal végzett műveletek elvégzését is magának kellett elvégeznie, ami így együtt bizony elég lassú volt. A mérnökök persze megértették a probléma lényegét, és létrehozták az FPU-t (Floating Point Unit, lebegőpontos egység, ami a 80-as évek végén még nem a CPU-ba volt építve, hanem egy külön processzor volt, mint most a gyorsabb GPU-k). Ezzel megoldották, hogy a számítógép külön program futtatása nélkül is képes legyen lebegőpontos számokkal műveleteket végezni. Így ezeket a feladatokat már nem a CPU, hanem az FPU-ba égetett kód végzi el.
Amint már megtudtuk, a lebegőpontos ábrázolás egyik feltétele, hogy a szám normalizált formában legyen felírva. Ez persze egy bizonyos érték után problémát okozhat, mert pl. olyan kicsi a szám, hogy a szükséges kitevőt már nem tudjuk felírni, vagyis az elérte minimális értékét. Ezt nevezzük alulcsordulásnak. Ilyenkor persze a mantissza bitszámán belül még közelebb kerülhetünk a nullához, ha a szám nem kerül normalizálásra. Ezt az állapotot nevezzük denormalizáltnak. Digitális audió esetén például akkor találkozhatunk denormalizációval, ha a DAW vagy a plugin nem kapcsolja ki a jelfeldolgozást, amikor az adott sávon (csatornán) nincsen adatáramlás, például leállítottuk a lejátszást.
Nagyon alacsony értékű lebegőpontos mintaértékek esetén az FPU ugyanolyan precizitással szeretne számolni, mint egyébként (vagyis nagyon pontosan), ehhez úgynevezett denormalizált módba vált. Ebben a módban azonos bitszám mellett sokkal pontosabban lehet nagyon kis számokat ábrázolni, mint a normalizált módban. A két mód közötti váltás, vagyis a szám átváltása, átkódolása, nagyon sok "időt" vesz igénybe, ami nagy CPU terhelést jelet. Ezek elsősorban hirtelen jelentkező tüske szerű terhelésekben jelentkeznek. Azt, hogy egy FPU mikor vált denormalizált módba, az FPU tervezője szabja meg, vagyis ez magába a csipbe van programozva (beégetve).
A hiba leginkább akkor keletkezik, amikor gyakorlatilag megszűnik a digitális jel (a mintaérték nulla), de előtte még volt ennél nagyobb érték, és a kettő között kell egy újabb értéket előállítani. Jellemző hiba ez késleltetőknél (delay), amikor a beérkező hang hirtelen megszűnik, de a késleltető részben a jelnek továbbra is folyamatosan halkulnia a kell. Vagyis a hang egyre halkabb és halkabb lesz, de a lebegőpontos ábrázolású extrém nagy felbontás miatt a nulla értéket elméletileg soha nem éri el. Vagyis a számot a végtelenségig próbálja például felezni. Ez elméletileg lehetséges, gyakorlatilag viszont nem. Mindez a látszólagos pontosság persze teljesen értelmetlen, mert a jelszint ilyenkor már olyan alacsony, hogy az egészből semmi sem hallható.
A jelenséget akkor tapasztalhatjuk, ha a DAW vagy a plugin nincsen erre a problémára felkészítve (nem megfelelő a szoftver programozása). Ilyenkor a hibás plugin lejátszás közben -amikor érkezik rá adat-, alacsony CPU felhasználást mutat, viszont amikor nem kap adatot, pl. leállítjuk a lejátszást, a CPU felhasználása folyamatosan nő, akár az összes rendelkezésre álló teljesítményt is felemésztheti.
A probléma megoldására több lehetőség is kínálkozik. A legegyszerűbb, ha maga a hardver kiszűri ezeket a hibákat, vagy ha már a szoftver kódjába elhelyezik a szükséges rutinokat, pl. olyat, ami időről időre lekérdezi, hogy az FPU éppen melyik módban van, és ha bekapcsolt a denormalizált mód -és ez egyébként szükségtelen-, akkor az értékeket egyszerűen nullára állítja át. Egy másik módszer, ha a plugin a bemenő jeltől függetlenül mindig előállít egy jelet (pl, zajt), ami olyan mintaértékkel rendelkezik, ami meghaladja a denormalizált mód bekapcsolásának szintjét, ezért az FPU soha nem fog ebbe a módba váltani. Ezt a megoldást kifejezetten ilyen célra készült pluginben is megtalálhatjuk, amit a hibás pluginek elé helyezve a denormalizációs hibát kiküszöbölhetjük. Ez a megoldás kissé hasonlít a dither-ben alkalmazott zajhoz.
Lebegőpontos ábrázolás előnyei
Természetesen az egyik előny a megnövekedett pontosság, amivel sokkal pontosabban tudjuk a digitalizált hangot feldolgozni, ami leginkább abban jelentkezik, hogy sokkal kevesebb lesz a zaj, és sokkal kevesebbet torzul a hullámforma csupán csak a kerekítési hibák miatt. Ez azonban sok esetben "direktben" nem hallható, inkább csak a hangzáson, a térbeliségen vesszük észre, és inkább csak az, akinek a hallása képes a finom részleteket megkülönböztetni. Ehhez persze megfelelő minőségű lehallgató rendszer is kell, amivel a legtöbb ember nem rendelkezik, még talán a stúdiók nagy részében sem. Ezért ettől az előnytől most tekintsünk el. Kipróbálhatjuk a dolgot, ha a DAW-ban 24 bites fixpontos, majd 32 (64) bites lebegőpontos feldolgozást és keverést állítunk be. Ha halljuk a különbséget, akkor jó. Ha nem halljuk, akkor nincsen sok értelme ezzel foglalkozni.
Tipp:
A mai korszerű i és xeon processzorok már olyan rendszerűek, hogy nincsen nagy különbség a fixpontos és lebegőpontos számítások elvégzési ideje között, sőt a 32 és 64 bit lebegőpont között sem tapasztalhatunk kétszeres különbséget, így amíg a gépünk bírja, semmi sem áll útjában, hogy használjuk őket. (Zárójelben jegyzem meg, hogy még ma sem képes minden plugin 64 bites pontossággal működni. Ez nem jelent problémát, mert mindkettő tudja fogadni a másik adatfolyamát, de a 32 bitesek esetében a 64 bites pontosság értelemszerűen elveszik. Figyelem! Itt most nem a 32 és 64 bites kódokról van szó, hanem a plugin belső számítási pontosságáról!)
Van viszont a lebegőpontos ábrázolásnak egy másik, sokkal inkább tapasztalható előnye, ez pedig nem a finom részletekben, hanem a magas mintaértékekben, vagyis a nagy jelszintekben tapasztalható. Ezzel talán már mindenki találkozott, amikor több sávot szeretett volna összekeverni, de az egyes buszokon, vagy a maszter buszon már megjelent a túlvezérlésre figyelmeztető jelzés.
És itt máris találkozhatunk egy általánosságban kevésbé értett jelenséggel. A legtöbb ember úgy gondolja, hogy a digitális 0 dBFS felett nincsen semmi. Ez -mint azt már többször említettem- a hardver oldalon igaz, de a szoftver oldalon nem, hiszen ha így lenne, nem látnánk a kivezérlésmérőkön 0 dBFS-nél magasabb értéket. Viszont látunk, és nem csak pár tized decibelt.
Végezzünk egy egyszerű próbát! Hozzunk létre a DAW-ban egy új projektet, amiben elhelyezünk egy új sávot (csatornát). A helyes értékek leolvasásához a panoráma korrekciót (pan law) állítsuk 0 dB-re, a feldolgozást pedig 32 bit lebegőpontosra. A sávra helyezzünk el egy hullámforma generátort, amin 440 Hz-es szinusz hullámot állítunk elő, méghozzá +1 dB-es kimeneti jelszinttel. (Már rögtön furcsa kéne hogy legyen, hogyan lehet 0 dBFS-nél magasabb értéket megadni!) Ha most megnézzük a sáv kivezérlésmérőjét, az +1 dB-t fog jelezni. Ez hogy lehet, mikor állítólag 0 dBFS felett nincsen semmi???
A válasz persze nagyon egyszerű, főleg azoknak, akik eddig figyeltek. A DAW ugyanis lebegőpontosan dolgozik, vagyis az ábrázolható értékek nagyobbak lehetnek, mint a 24 biten ábrázolhatóak. Tehát könnyű szerrel képes a jelszint 0 dBFS fölé menni, és persze nem csak úgy valamennyivel, hanem a DAW mindig egészen pontosan tudja azt is, hogy mennyivel. Máskülönben nem lenne értelme az egésznek. Mint a példából is láthattuk, a szoftver oldalon (ha lebegőpontos ábrázolást használunk), a jelszint képes meghaladni a 0 dBFS értéket, viszont a hardver oldalon, vagyis az analóg jellé alakítás közben már nem! Erre figyelmeztet a túlvezérlésjelző vörös szín (lásd később).
Mivel a DAW nem csak azt tudja, hogy 0 dBFS fölé ment a jelszint, hanem minden mintaérték esetében azt is hogy mennyivel, így több sávból összeadódó túlvezérlés a DAW-on belül gyakorlatilag soha nem jön létre. A "gyakorlati" szó alatt a 32 bites lebegőpontos ábrázolással elérhető 1528 dB-es dinamikatartományt értsük, ami a 0 dBFS-hez mért -758 dB zajküszöbből és +770 dB maximális jelszintből tevődik össze. A Földön tapasztalható hangnyomás különbség maximális értéke kb. 190 dB (lásd lejjebb), ami jóval a fent említett 1528 dB-es dinamikatartományon belül helyezkedik el, vagyis normál esetben soha nem érjük el a 32 bites lebegőpontos ábrázolás határait. Tehát a mintaérték a gyakorlatban nem csak hogy nem haladja meg a 32 bit FP maximális értéket, de el sem éri azt. Így aztán a létrejövő adatvesztések nem a túlvezérlésből adódó jelcsúcs levágások miatt történnek.
Tipp:
Hogyan számítható ki a Földön tapasztalható hangnyomásszint dinamikatartomány értéke? Nagyon egyszerűen! A lehetséges maximális hangnyomásszintből kivonjuk a minimális hangnyomásszintet. Mennyi a maximum? Mivel a hang a levegőrészecskék longitudinális mozgásából adódik, így erősen kötődik a levegő részecskéihez. A levegő molekuláinak is van mérete és tömege, valamint hat rájuk is a tömegvonzás. Mindezekből kiszámítható, hogy a Föld atmoszférájában létrejönni képes legnagyobb hangnyomásszint 194 dB SPL. Az a légnyomás változás, ami ennél nagyobb erővel mozgatja meg a részecskéket, már nem hullámként -vagyis hangként- terjed, hanem magával mozdítja a levegőt is. Ebben az esetben már nem hangról, hanem lökéshullámról beszélünk. Mennyi a minimum? A Földön tapasztalható legalacsonyabb hangnyomásszintek az úgynevezett visszaverődés mentes helyiségekben alakulnak ki. Ezek értéke általában 4 dB SPL. 194-4=190 dB.
Nézzük most ezt meg egy kicsit gyakorlatiasabb példán keresztül. Az előző projektet egészítsük most ki két újabb csatornával, és küldjük ide SEND-en keresztül a már létrehozott szinusz hullámos csatorna jelét, miközben a hanggenerátoros csatornát kössük le a maszter buszról. (Vagyis a szinusz hullám csak a két újonnan létrehozott csatornán keresztül juthat a maszter buszra. Erre azért van szükség, mert ha két külön hullámforma generátort használnánk, akkor semmi sem biztosítaná, hogy a kettő szinkronban működik. Ilyenkor a két hullámforma fázisa eltérő lehet, amitől azok nem összeadódnak, hanem kivonódnak egymásból, vagyis a jel kisebb szintű lesz, nem nagyobb.) Az egyszerűbb számolhatóság miatt a hullámforma generátor kimeneti jelszintjét állítsuk most 0dB(FS)-re. Ha mindent jól csináltunk, akkor az új csatornákon 0dBFS jelszintet mérünk, a maszter buszon pedig +6dBFS-t. Helyezzünk most el a két új csatornára és a maszter buszra is egy-egy oszcilloszkóp plugint, amin megvizsgálhatjuk a hullámformánk alakját. Én az ingyenes MOscilloscope-ot ajánlom, mert ezt bármelyik DAW-ban használhatjuk. Figyeljünk rá, hogy a szürke ablak jobb felső részében lévő "normalize" és "normalize above 0dB" kapcsolók ne legyenek benyomva (lásd a mellékelt ábrán)!
Mit láthatunk? Gyakorlatilag azt, ami várható volt. A 2 és 3 csatornákon (az újonnan létrehozott csatornák) a torzítatlan szinusz hullám érkezik (és távozik is), 0 dBFS-re kivezérelve. Ezek a maszter buszon összegződnek, így a jelszint +6dBFS-lesz, ami már nem ábrázolható 0 dBFS-ig, hiszen meghaladja azt. Ennek következtében -a hardver eszközökhöz hasonlóan- a jelcsúcs levágódik, mint az a harmadik ábrán is látható. Tehát ebben az esetben a maszter buszra érkező jel szintje meghaladta a 24 bit fixponton ábrázolható maximális értéket, vagyis túlvezérlés keletkezik, ezért vágódik le a szinusz felső és alsó része, és ezért világít a túlvezérlésjelző vörös fénnyel (amiben szintén látható a +6 dB érték). A konverter kimenetén ez tehát torzított hangként fog megjelenni.
Mit kell tennünk ahhoz, hogy meglássuk, hogy ez a torzított jel milyen frekvencia összetevőkkel rendelkezik? Elhelyezünk egy spektrumanalizátor plugint a maszter sávra! -gondolja az egyszeri hangmérnök... Ám amikor ezt megteszi, meglepő módon csak egyetlen frekvenciát lát a kijelzőn, méghozzá 440 Hz-en. Akkor most mi van? -kérdezi, hiszen az eddigi tanulmányok alapján a maszter buszon látható hullámforma felharmonikusokban gazdag spektrumeloszlást kéne hogy mutasson. Hát igen, itt jön be a lebegőpontos ábrázolás lényege. Hagyjunk most ki egy lépést ahhoz, hogy megértsük a dolgokat, és szimuláljuk a 24 bites fixpontos ábrázolást (mint ahogyan egy DA konverter előállítaná ezt a torzított szinuszt). Ehhez helyezzünk el az oszcilloszkóp után egy bitcsökkentő plugint, amit 24 bit fixpontra állítunk be (A dithert kapcsoljuk ki! lásd a mellékelt ábrán), és csak ez után helyezzük el a spektrumanalizátort. Vagyis most már a valódi 24 bites fixpontos spektrum képet fogjuk látni.
Meg is vannak a felharmonikusok, ahogy annak lennie kell. Aki egy kicsit szemfülesebb, már kapizsgálhatja, hogy mit is nyerhetünk a lebegőpontos ábrázolással és az általa nyújtott megnövekedett dinamikatartománnyal.
A példa alapján tehát azt gondolhatjuk, hogy a maszter buszon összegzett szinusz hullám már eltorzult, hiszen átlépte a 0 dBFS jelszintet, ami felett pedig nincsen semmi, ezért levágódnak a 0 dBFS fölé eső részek. Ez fixpontos ábrázolásnál igaz, lebegőpontos ábrázolásnál csak akkor, ha direkt ilyen funkciót állítunk be. A legtöbb DAW a csatornákon belüli számításokat lebegőpontosan végzi el, függetlenül attól, hogy milyen keverési bitmélységet állítottunk be. Ilyen pl. a Reaper is, bár most a keverést is lebegőpontosra kértük a projekt létrehozásakor (ez egyébként az alapbeállítás is, tehát külön nem kell kiválasztani). Mire jó mindez? Jöjjön akkor a csoda, amihez nem kell más, mint egy jelszint beállító plugin (vagy olyan, amin van ilyen jellegű poti). Az egyszerűség és a platformfüggetlenség miatt használjuk most az ingyenes MEqualizer-t, ami egy EQ plugin, de lehet vele halkítani és hangosítani is. Helyezzük el ezt az első insert pontra, vagyis az oszcilloszkóp plugin elé!
Mint látható, az MEqualizer analizátorán nem láthatjuk a torzításból eredő felharmonikusokat, és ebből sokan talán már sejtik, hogy azért, mert itt még lebegőpontos az ábrázolás, és ennek köszönhetően nem vágódnak le a 0dBFS feletti mintaértékek. Hogy miért látszik a spektrumanalizátoron mégis tökéletes kép? Mert az MEqualizer alapbeállítása szerint 0dBFS-re normalizálja a képen látható jelet, ezért nem vágódik le a frekvenciatüske csúcsa. Ha kikapcsoljuk a normalizálást, akkor rögtön vágott jelet láthatunk, de ennek a mi szempontunkból most nincsen jelentősége.
Kezdjük most csökkenteni az MEqualizerből kilépő, lebegőpontosan ábrázolt jelszintet az "OUTPUT" poti letekerésével. Hogy ne maradjunk le a csodáról, közben erősen figyeljük a maszter buszra elhelyezett oszcilloszkóp képét is! Mint láthatjuk, a jelszint csökkenésével kezd eltűnni a jelcsúcs vágása is, és ezzel együtt a kialakult felharmonikusok is. Ha elérjük a -6dB értéket, már az eredeti, torzítatlan szinusz hullámot kapjuk vissza, és a spektrumanalizátorok is azonos képet mutatnak. (Miért pont -6dB? Mert két 0 dBFS jel összege +6 dBFS, tehát ezt kell kompenzálni.) Vagyis bizonyítottuk, hogy a lebegőpontos ábrázolásnak köszönhetően a 0 dBFS feletti értékek nem vágódnak le (egészen +770 dBFS-ig), vagyis ha kompenzáljuk a létrejött túlvezérlést, nem történik adatvesztés mindaddig, amíg el nem hagyjuk a szoftver oldalt. Ha azt gondoljuk, hogy ez csak +6dB-ig működik, akkor bátran többszörözzük meg a bemenő jelet akár szintemeléssel, akár a sávok számának növelésével, majd kompenzáljunk a maszter busz bemenetén. Ehhez egy érték után már nem elegendő egyetlen jelszint csökkentő plugin, de annyit használhatunk, amennyit csak a DAW elbír, a jel minősége nem fog számottevően csökkenni.
Tipp:
Léteznek bizonyos algoritmusok (audio declipper), amik egyfajta interpolációval és mesterséges intelligenciával megpróbálják kitalálni, hogy mi lehetett a levágott részeken, de gondolom az mindenki számára világos, hogy ott bármi lehetett, így a kitalációk jó esetben is csak megközelíthetik a valóságot, az eredeti hullámformát visszaállítani elméletileg lehetetlen. Jusson mindez eszünkbe, amikor figyelmen kívül hagyjuk a maszter sávon megjelenő túlvezérlésre figyelmeztető jelzést!
Mit állapíthattunk meg mindebből? Fixpontos ábrázolás esetében 0 dBFS-ig nem jön létre torzítás (legalábbis nem túlvezérlés következtében), sem a sávokon, sem a buszokon, vagy a maszter buszon. Lebegőpontos ábrázolás esetén +750 dBFS-ig sem a sávokon, sem a buszokon, sem a maszter buszon nem jön létre visszaállíthatatlan torzítás, ha túlvezérlés keletkezik. Erre azonban a DAW kivezérlésmérők minden esetben figyelmeztetnek. Ilyenkor nincsen más dolgunk, csak csökkenteni a jelszintet (vagy jelszinteket) mindaddig, amíg az 0 dBFS alá nem csökken. Ha ezt nem tesszük meg, akkor fixpontos ábrázolás esetén (például régi pluginek, vagy exportálás) a túlvezérlésből eredő jelcsúcsvágások nem visszafordíthatóak. Ha viszont lebegőpontos ábrázolást használunk, akkor megfelelő jelszintcsökkentéssel az eredeti hullámforma gyakorlatilag mindig visszaállítható.
Tehát kijelenthetjük, hogy ha erre felkészített szoftvereket használunk, akkor a túlvezérlésmérőkön jelzett túlvezérlés nem jelent minőségcsökkenést, sem pedig adatvesztést mindaddig, amíg a jelszint ábrázolható a rendelkezésre álló lebegőpontos biteken, és a digitális tartományon belül maradunk (lebegőpontos adattovábbítás és feldolgozás). Szintén nem történik jelentős torzítás, amennyiben a DAW elhagyása előtt (DA konverter vagy fixbites render) a jelszintet csökkentjük a szükséges értékre (24 vagy 16 bit fixpontos ábrázolás). A megfelelő kompenzációs érték (jelszintcsökkentés) megtalálásában segít a maszter busz túlvezérlésjelzője!
Analóg modellezett pluginek
Bár szinte minden analóg modellezett plugin képes lebegőpontos működésre, a 0 VU jelszintjük (az optimális működési szint) általában -18 dBFS RMS-re van kalibrálva (vagy mi magunk állíthatjuk be a 0VU értékét). Ez azt jelenti, hogy ezen a jelszinten ugyanolyan torzítást állítanak elő, mint amit az általuk utánzott hardvereszköz okozna ugyanilyen jelszinten. Egyértelmű, hogy minél magasabb jelszintet kapnak, annál nagyobb lesz a torzításuk, akárcsak az analóg megfelelőiknek. Az, hogy a pluginre akár +100 dB-t is ráküldhetünk, nem azt jelenti, hogy ilyen magas értéken is ugyanúgy fog torzítani, mint a beállított 0 VU-nak megfelelő dBFS értéken, hiszen ilyenkor a jelszint 100 dB-el magasabb, mint amit a valóságban kapna, vagyis jelentősen nagyobb torzítást fog létrehozni. (Ebben eltér a hardver megfelelőjétől, ami nagy valószínűséggel ilyen jelszintnél már kigyulladna.) Vagyis a "korlátlan" jelszintet csak az úgynevezett "teljesen digitális" pluginekben tudjuk megfelelően kihasználni, amik nem szimulálnak analóg torzításokat, ezekben viszont az 1500 dB-es dinamikatartomány miatt nem kell tartanunk a túlvezérlés okozta torzításoktól.
A számítógépek jelenleg csak kettes számrendszerben képesek működni, vagyis adatokat tárolni, mozgatni és számolni. Ez azt jelenti, hogy bármennyi bitet is használunk az adat ábrázolására, az a hardver szintjén csak egész szám lehet. Az egyszerűség kedvéért vegyünk egy 2 bites példát. Itt ugye az első bit (LSB) tízes számrendszerre váltva lehet 0 vagy 1, a második bit pedig 0 vagy 2. Tehát 2 biten ábrázolhatjuk a következő decimális számokat: 0, 1, 2, 3. Vagyis nem ábrázolhatunk 1,5-öt, vagy 0,3-at. Ez miért probléma?
A hangerő csökkentése nem más, mint a pillanatnyi feszültségértékek csökkentése. Ez nyilvánvaló, hiszen a halkabb hang a legtöbbször alacsonyabb feszültségértéket is jelent. Ha a jelszintet a felére szeretnénk csökkenteni, akkor a feszültségértéket is a felére kell csökkenteni, vagyis osztani kell kettővel. Pontosan ez is történik, a DAW minden minta értéket eloszt kettővel. Ha csak páros számok szerepelnek a mintákban, nincsen nagy gond, hiszen ezeket kettővel osztva minden esetben egész számot kapunk, ami könnyedén felírható fixpontos ábrázolással. Na de mi van akkor, ha a minta értéke mondjuk 3? Annak a fele 3/2, vagyis 1,5, ami nem egész szám, tehát a fenti rendszerben nem tudjuk ábrázolni. Ahhoz, hogy az eredménynek legalább egy része megmaradjon, kerekítenünk kell. Ebben az esetben vagy 1, vagy 2 lesz a kapott érték, az osztó algoritmus programozása szerint. A művelet során tehát ugyanolyan kerekítési, vagyis kvantálási hiba keletkezik, mint digitalizáláskor, és mint már tudjuk, ez további kvantálási zajhoz és torzításhoz vezet. Mindennek tetejébe, minél több ilyen törtszámot eredményező műveletet végzünk el, annál több és annál nagyobb hibát viszünk bele a hangba, vagyis a hiba folyamatosan erősödik.
Megoldás lehet, ha az egyes értékeket kódolva ábrázoljuk. Ez jelentheti például azt, hogy létrehozunk egy képzeletbeli tizedes jelzőt, amivel elkülönítjük a tizedes számokat az egész számoktól, akárcsak a hétköznapi matematikában. Ezt a tizedespontot a választott bitmélységen ábrázolható számok egy bizonyos pontjára helyezzük el, így már képesek leszünk tizedes értékeket is ábrázolni, viszont ezzel együtt csökken a szám egészének ábrázolására használható bitek száma. Nézzünk egy példát! Maradjuk az előző 2 bites esetnél, ahol most a jobbra eső bit lesz a tizedes jegy. Ebben az esetben ábrázolható számok: 0, 1, 0,1 és 1,1. Nem sok, de több mint a semmi. Persze ha több bitet használunk és több bitet engedünk át a tizedes jegyeknek, akkor még finomabb ábrázolást is elérhetünk, de minden esetben csökken a maximálisan ábrázolható érték. Megoldás lehet persze az is, ha a tizedes jegyeket kódoljuk, például a fenti esetben a jobbra eső bit 1 értéke 0,5-öt jelent. Ilyenkor már ábrázolhatjuk a fél számokat is. Ebben az esetben persze minden művelet elvégzése előtt és után is kódolnunk kell, ami persze extra idő elhasználását jelenti. Ennek a megoldásnak egy további óriási hátránya, hogy csak előre meghatározott számú tizedest tudunk használni. Ez két okból probléma: 1. ha ezekre nincsen szükség, akkor csak feleslegesen foglalják a helyet, 2. ha túl kevés a tizedes, akkor szintén kerekítési problémába ütközünk. Egy másik probléma, hogy a rögzített tizedesek elveszik a helyet a nagy számok ábrázolásától. Vagyis se nagy számokat, se kis számokat nem tudunk korlátlan (vagy legalábbis közel korlátlan) pontossággal ábrázolni.
Hasonlóan működik a lebegőpontos ábrázolás a számítógépek esetében is, de itt nem tízes, hanem kettes számrendszerben dolgozunk. Mint látható, ez is egyfajta kódolt szám, és mint ilyen, sajnos többféle változata létezik, attól függően, hogy ki írta a programot. Ebből adódik, hogy néhány esetben a lebegőpontos fájlok nem kompatibilisek az egyes DAW-ok között. A legelterjedtebb szabvány az ANSI/IEEE Std. 754-1985, ami két ábrázolást ír le. Az egyik a 32 bites lebegőpontos, amit normál pontosságúnak neveznek, és a 64 bites lebegőpontos, amit dupla pontosságúnak.
Mint ahogy az ábrán is látszik, a 32 bitet három csoportra osztjuk fel. 0-22 bitek alkotják a mantisszát, 23-30 bitek a kitevőt, és a 31-es bit pedig az előjelet. Ezek együtt határozzák meg a 32 bites lebegőpontos szám valódi értékét (v), mégpedig a következő képlet alapján, ahol (-1)^S (az előjel bit (S)) jelzi, hogy a szám pozitív vagy negatív. Ha a bit 0, akkor a szám pozitív, ha 1, akkor negatív. Az "E" a kitevőben lévő érték, ami 0-255 lehet. Mivel ebből kivonunk 127-et, így lehetővé válik, hogy a 2 hatvány kitevője -127 és +128 között változzon (vagyis az értéket eltolt bináris formában tároljuk). Az egyenletben az "M" jelöli a mantisszát, normalizált tört értékként ábrázolva. Decimális ábrázoláskor például a 2,783 jelentése: 2 + 7/10 + 8/100 + 3 /1000. Bináris alakban az 1.0101 értéke hasonlóan alakul ki, de nem tízes, hanem kettes kitevővel dolgozunk, tehát a valódi érték 1 + 0/2 + 1/4 + 0/8 + 1/16.A normalizáció ugyanúgy történik meg, mint a tudományos ábrázolásnál, vagyis csak egyetlen nem nulla számjegy maradhat a tizedesjegy előtt (a bal oldalon, amit a kettes számrendszerben kettesjegynek, bináris pontnak hívunk). Mivel a kettes számrendszerben csak egyetlen egy, nem nulla számjegy létezik, az 1, így ezt nem is kell ábrázolnunk, ezzel máris megspóroltunk egy bitet. A mantissza értékét tehát a következő képlettel kapjuk meg: M=1 + m22^-1 + m21^-2 + m20^-3... Ha a 0-22. bitek mind nulla értékűek, akkor a mantissza értéke 1. Ha a 0-22. bitek mind 1 értékűek, akkor a mantissza értéke éppen egy hajszálnyival van 2 alatt, pontosan: 2-2^-23.
Az IEEE 754-1985. szabvány szerint ábrázolható legkisebb és legnagyobb érték azonban nem egyezik az elérhető maximális értékekkel, mert bizonyos számokat speciális jelentéssel ruháztak fel. Ha a mantissza és a kitevő összes bitje 0 értékű, akkor a valódi érték +/-nulla. Ha az összes mantissza bit nulla, és az összes kitevő bit 1, akkor a valódi érték +/-végtelen. Emellett néhány nagyon kicsi normalizálatlan szám is bekerült a csoportba, méghozzá +/- 1,2x10^-38 és +/- 1,4x10^-45 között. Ezek alacsony pontossággal ábrázolt számok, amiket akkor kapunk, ha nem tartjuk be azt a szabályt, hogy a mantissza első számjegye 1 kell hogy legyen. Ezen a három fő csoporton kívül is vannak bizonyos minta szerű kivételek, amiknek nincsen jelentése, egyszerűen csak "nem számoknak", angolul NAN-nak (Not A Number) nevezték el őket. Mindezek figyelembevételével a legnagyobb ábrázolható szám +/- 3,4x10^38, a legkisebb pedig +/- 1,2x10^-38.
A szabvány szerinti dupla pontosságú, 64 bites lebegőpontos ábrázolás ugyanígy működik, de 52 bites mantisszával és 11 bites kitevővel. Gyakorlatilag elmondható, hogy már a 32 bites lebegőpontos ábrázolás alkalmazásával sem nagyon találni olyan feladatot amire az ne lenne elég, az viszont biztos, hogy a 64 bites változat esetében ilyen feladat nem is létezik. Biztos ami biztos alapon azonban a szabványt már most felkészítették a 128 és 256 bites ábrázolásra is.
Lebegőpontos ábrázolás problémái
Sajnos bármilyen hihetetlen pontossággal is képesek a lebegőpontos számok ábrázolni a valódi értékeket, azok minden esetben kerekítésre kerülnek, hiszen a mantissza sem áll végtelen számú bitből (ha abból állna, akkor végtelen sokáig tartana kiszámolni, elmenteni, majd újból előhívni, így végtelen sokat kéne várnunk, amíg csak egyetlen minta is elkészülne). Tehát itt sem szabadultunk meg a konvertereket, és egyéb fixpontos ábrázolást használó szoftvereket sújtó kvantálási hibáktól, egyszerűen csak más formába öntöttük őket.
A lebegőpontos ábrázolás "hibája", hogy valójában nem a felbontást növeli meg, hanem a szám ábrázolásához használt "arányt" változtatja. Ez azt jelenti, hogy egy adott kitevő esetén, az ábrázolható számok között nem végtelenül kicsi a különbség, hanem az ábrázolt számtól, vagyis a kitevőtől függően változik. Általában az ábrázolt szám tízmilliomod részéről beszélhetünk, egészen pontosan 2^-24 és 2^-23 között változik. Ha pl. a kitevő alacsony értékű, akkor csak kis értékű számokat tudunk ábrázolni, viszont az ábrázolható számok között nagyon kicsi lehet a különbség is (lásd a zöld mezőben). Ha viszont az ábrázolni kívánt szám nagy, akkor a számmal együtt az egyes számok közötti különbség is megnő, vagyis egy bizonyos szempontból kevésbé részletes ábrázolás történik (vörös mezőben).
A kerekítési hibák mértéke tehát attól függ, hogy éppen mekkora számmal dolgozunk. Ha nagy számokkal, akkor az abszolút eltérés nagy lesz, ha kicsikkel, akkor kicsi. A relatív eltérés persze azonos marad, de kérdés persze, hogy például kicsi számok esetén megengedhető-e az a kis eltérés is? Ilyen pl. az 1,1, ami pont két lebegőpontosan ábrázolható szám közé esik: 1.0999999046 és 1.1000000238. Mint látható, az eltérés nem nagy, persze kérdés, hogy mihez képest...
Hogy magunk is meggyőződhessünk a lebegőpontos "pontatlanságról", végezzünk el két próbát. Most nem a DAW-ban, hanem egy online BASIC nyelvet használó program-futtató környezetben fogunk dolgozni, amit ide kattintva érhetünk el. Megnyitás után töröljünk mindent a "Source Code" mezőből, és másoljuk be a következő pár sort (CTRL+C és CTRL+V).
 |
| Ezt kéne kapnunk, de ... |
110 FOR X = 0 TO 10 STEP 0.01
120 PRINT X
130 NEXT X
A program első sorában egy úgynevezett ciklust hozunk létre, ami 0-tól 10-ig növeli X értékét, méghozzá úgy, hogy minden újabb ciklusban 0,01-et ad X aktuális értékéhez. A 0,01 egy tört szám, vagyis lebegőpontosan kell ábrázolni, tehát a vele végzett műveletek is lebegőpontosan mennek végbe! A következő sorban kiíratjuk X aktuális értékét, majd a 130-as sorban visszaugrunk a 110-es sorra, és a ciklus újból indul, amíg X értéke el nem éri a 10-et.
Mit kéne látnunk, ha majd elindítjuk a programot? Szerintem ez nagyon egyszerű, és gondolom az olvasók is kitalálták már, egy számsort kell hogy kapjunk, pontosan olyat, mint ami a baloldali ábrán látható.
 |
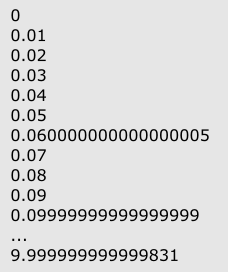| ... ezt kapjuk. |
Mint látható, a lebegőpontos ábrázolás miatt bekövetkező kerekítési hibák bizony eléggé eltérő eredményt adnak ahhoz képest, mint amit matematikailag várnánk. A legmeglepőbb, hogy a ciklus el sem érte a 10-et mielőtt leállt volna. Ezt az összeadódó kerekítési hibáknak köszönhetjük, ugyanis ezeknek köszönhetően X az utolsó ciklus előtt 10.000133-as értéket ért el, ami nagyobb mint 10, ezért a program még az előtt leállt, hogy kiírhatta volna a 10-et. Ez a befejezetlen ciklus egy jellegzetes hiba a számítógépes programokban.
Ha 32 bites lebegőpontos ábrázolásról beszélünk, akkor amíg 24 biten is ábrázolható az adott szám (+/- 2^24, vagyis elfér a mantisszában), és ráadásul egész is, nincsen probléma, ugyanis ezek között a számok között a különbség mindig 1. Az így ábrázolható számok esetében tehát a kerekítés nem ad hibát. (Ha végig gondoljuk mindezt, akkor eltöprenghetünk azon, hogy vajon érdemes-e a 24 bites fixpontosan digitalizált (tehát csak egész számokat tartalmazó hangunkat) lebegőpontossá alakítva feldolgozni...) Ha viszont ennél nagyobb számokról van szó, amit már csak lebegőpontosan tudunk ábrázolni, akkor a különbség az egyes számok között változóvá válik, ezért a számítások elvégzése után végzett kerekítések alkalmával egyes számok kimaradhatnak.
Denormalizációs hiba (denormal)
Régebben a CPU-nak nem csak a program futtatását, de a lebegőpontos számokkal végzett műveletek elvégzését is magának kellett elvégeznie, ami így együtt bizony elég lassú volt. A mérnökök persze megértették a probléma lényegét, és létrehozták az FPU-t (Floating Point Unit, lebegőpontos egység, ami a 80-as évek végén még nem a CPU-ba volt építve, hanem egy külön processzor volt, mint most a gyorsabb GPU-k). Ezzel megoldották, hogy a számítógép külön program futtatása nélkül is képes legyen lebegőpontos számokkal műveleteket végezni. Így ezeket a feladatokat már nem a CPU, hanem az FPU-ba égetett kód végzi el.
 |
| Intel 80386 CPU és a hozzá tartozó 387DX matematikai segédprocesszor (Co-processor, vagy FPU) |
Nagyon alacsony értékű lebegőpontos mintaértékek esetén az FPU ugyanolyan precizitással szeretne számolni, mint egyébként (vagyis nagyon pontosan), ehhez úgynevezett denormalizált módba vált. Ebben a módban azonos bitszám mellett sokkal pontosabban lehet nagyon kis számokat ábrázolni, mint a normalizált módban. A két mód közötti váltás, vagyis a szám átváltása, átkódolása, nagyon sok "időt" vesz igénybe, ami nagy CPU terhelést jelet. Ezek elsősorban hirtelen jelentkező tüske szerű terhelésekben jelentkeznek. Azt, hogy egy FPU mikor vált denormalizált módba, az FPU tervezője szabja meg, vagyis ez magába a csipbe van programozva (beégetve).
A hiba leginkább akkor keletkezik, amikor gyakorlatilag megszűnik a digitális jel (a mintaérték nulla), de előtte még volt ennél nagyobb érték, és a kettő között kell egy újabb értéket előállítani. Jellemző hiba ez késleltetőknél (delay), amikor a beérkező hang hirtelen megszűnik, de a késleltető részben a jelnek továbbra is folyamatosan halkulnia a kell. Vagyis a hang egyre halkabb és halkabb lesz, de a lebegőpontos ábrázolású extrém nagy felbontás miatt a nulla értéket elméletileg soha nem éri el. Vagyis a számot a végtelenségig próbálja például felezni. Ez elméletileg lehetséges, gyakorlatilag viszont nem. Mindez a látszólagos pontosság persze teljesen értelmetlen, mert a jelszint ilyenkor már olyan alacsony, hogy az egészből semmi sem hallható.
A probléma megoldására több lehetőség is kínálkozik. A legegyszerűbb, ha maga a hardver kiszűri ezeket a hibákat, vagy ha már a szoftver kódjába elhelyezik a szükséges rutinokat, pl. olyat, ami időről időre lekérdezi, hogy az FPU éppen melyik módban van, és ha bekapcsolt a denormalizált mód -és ez egyébként szükségtelen-, akkor az értékeket egyszerűen nullára állítja át. Egy másik módszer, ha a plugin a bemenő jeltől függetlenül mindig előállít egy jelet (pl, zajt), ami olyan mintaértékkel rendelkezik, ami meghaladja a denormalizált mód bekapcsolásának szintjét, ezért az FPU soha nem fog ebbe a módba váltani. Ezt a megoldást kifejezetten ilyen célra készült pluginben is megtalálhatjuk, amit a hibás pluginek elé helyezve a denormalizációs hibát kiküszöbölhetjük. Ez a megoldás kissé hasonlít a dither-ben alkalmazott zajhoz.
Lebegőpontos ábrázolás előnyei
Természetesen az egyik előny a megnövekedett pontosság, amivel sokkal pontosabban tudjuk a digitalizált hangot feldolgozni, ami leginkább abban jelentkezik, hogy sokkal kevesebb lesz a zaj, és sokkal kevesebbet torzul a hullámforma csupán csak a kerekítési hibák miatt. Ez azonban sok esetben "direktben" nem hallható, inkább csak a hangzáson, a térbeliségen vesszük észre, és inkább csak az, akinek a hallása képes a finom részleteket megkülönböztetni. Ehhez persze megfelelő minőségű lehallgató rendszer is kell, amivel a legtöbb ember nem rendelkezik, még talán a stúdiók nagy részében sem. Ezért ettől az előnytől most tekintsünk el. Kipróbálhatjuk a dolgot, ha a DAW-ban 24 bites fixpontos, majd 32 (64) bites lebegőpontos feldolgozást és keverést állítunk be. Ha halljuk a különbséget, akkor jó. Ha nem halljuk, akkor nincsen sok értelme ezzel foglalkozni.
Tipp:
A mai korszerű i és xeon processzorok már olyan rendszerűek, hogy nincsen nagy különbség a fixpontos és lebegőpontos számítások elvégzési ideje között, sőt a 32 és 64 bit lebegőpont között sem tapasztalhatunk kétszeres különbséget, így amíg a gépünk bírja, semmi sem áll útjában, hogy használjuk őket. (Zárójelben jegyzem meg, hogy még ma sem képes minden plugin 64 bites pontossággal működni. Ez nem jelent problémát, mert mindkettő tudja fogadni a másik adatfolyamát, de a 32 bitesek esetében a 64 bites pontosság értelemszerűen elveszik. Figyelem! Itt most nem a 32 és 64 bites kódokról van szó, hanem a plugin belső számítási pontosságáról!)
Van viszont a lebegőpontos ábrázolásnak egy másik, sokkal inkább tapasztalható előnye, ez pedig nem a finom részletekben, hanem a magas mintaértékekben, vagyis a nagy jelszintekben tapasztalható. Ezzel talán már mindenki találkozott, amikor több sávot szeretett volna összekeverni, de az egyes buszokon, vagy a maszter buszon már megjelent a túlvezérlésre figyelmeztető jelzés.
És itt máris találkozhatunk egy általánosságban kevésbé értett jelenséggel. A legtöbb ember úgy gondolja, hogy a digitális 0 dBFS felett nincsen semmi. Ez -mint azt már többször említettem- a hardver oldalon igaz, de a szoftver oldalon nem, hiszen ha így lenne, nem látnánk a kivezérlésmérőkön 0 dBFS-nél magasabb értéket. Viszont látunk, és nem csak pár tized decibelt.
A válasz persze nagyon egyszerű, főleg azoknak, akik eddig figyeltek. A DAW ugyanis lebegőpontosan dolgozik, vagyis az ábrázolható értékek nagyobbak lehetnek, mint a 24 biten ábrázolhatóak. Tehát könnyű szerrel képes a jelszint 0 dBFS fölé menni, és persze nem csak úgy valamennyivel, hanem a DAW mindig egészen pontosan tudja azt is, hogy mennyivel. Máskülönben nem lenne értelme az egésznek. Mint a példából is láthattuk, a szoftver oldalon (ha lebegőpontos ábrázolást használunk), a jelszint képes meghaladni a 0 dBFS értéket, viszont a hardver oldalon, vagyis az analóg jellé alakítás közben már nem! Erre figyelmeztet a túlvezérlésjelző vörös szín (lásd később).
Mivel a DAW nem csak azt tudja, hogy 0 dBFS fölé ment a jelszint, hanem minden mintaérték esetében azt is hogy mennyivel, így több sávból összeadódó túlvezérlés a DAW-on belül gyakorlatilag soha nem jön létre. A "gyakorlati" szó alatt a 32 bites lebegőpontos ábrázolással elérhető 1528 dB-es dinamikatartományt értsük, ami a 0 dBFS-hez mért -758 dB zajküszöbből és +770 dB maximális jelszintből tevődik össze. A Földön tapasztalható hangnyomás különbség maximális értéke kb. 190 dB (lásd lejjebb), ami jóval a fent említett 1528 dB-es dinamikatartományon belül helyezkedik el, vagyis normál esetben soha nem érjük el a 32 bites lebegőpontos ábrázolás határait. Tehát a mintaérték a gyakorlatban nem csak hogy nem haladja meg a 32 bit FP maximális értéket, de el sem éri azt. Így aztán a létrejövő adatvesztések nem a túlvezérlésből adódó jelcsúcs levágások miatt történnek.
Tipp:
Hogyan számítható ki a Földön tapasztalható hangnyomásszint dinamikatartomány értéke? Nagyon egyszerűen! A lehetséges maximális hangnyomásszintből kivonjuk a minimális hangnyomásszintet. Mennyi a maximum? Mivel a hang a levegőrészecskék longitudinális mozgásából adódik, így erősen kötődik a levegő részecskéihez. A levegő molekuláinak is van mérete és tömege, valamint hat rájuk is a tömegvonzás. Mindezekből kiszámítható, hogy a Föld atmoszférájában létrejönni képes legnagyobb hangnyomásszint 194 dB SPL. Az a légnyomás változás, ami ennél nagyobb erővel mozgatja meg a részecskéket, már nem hullámként -vagyis hangként- terjed, hanem magával mozdítja a levegőt is. Ebben az esetben már nem hangról, hanem lökéshullámról beszélünk. Mennyi a minimum? A Földön tapasztalható legalacsonyabb hangnyomásszintek az úgynevezett visszaverődés mentes helyiségekben alakulnak ki. Ezek értéke általában 4 dB SPL. 194-4=190 dB.
Mit láthatunk? Gyakorlatilag azt, ami várható volt. A 2 és 3 csatornákon (az újonnan létrehozott csatornák) a torzítatlan szinusz hullám érkezik (és távozik is), 0 dBFS-re kivezérelve. Ezek a maszter buszon összegződnek, így a jelszint +6dBFS-lesz, ami már nem ábrázolható 0 dBFS-ig, hiszen meghaladja azt. Ennek következtében -a hardver eszközökhöz hasonlóan- a jelcsúcs levágódik, mint az a harmadik ábrán is látható. Tehát ebben az esetben a maszter buszra érkező jel szintje meghaladta a 24 bit fixponton ábrázolható maximális értéket, vagyis túlvezérlés keletkezik, ezért vágódik le a szinusz felső és alsó része, és ezért világít a túlvezérlésjelző vörös fénnyel (amiben szintén látható a +6 dB érték). A konverter kimenetén ez tehát torzított hangként fog megjelenni.
Mit kell tennünk ahhoz, hogy meglássuk, hogy ez a torzított jel milyen frekvencia összetevőkkel rendelkezik? Elhelyezünk egy spektrumanalizátor plugint a maszter sávra! -gondolja az egyszeri hangmérnök... Ám amikor ezt megteszi, meglepő módon csak egyetlen frekvenciát lát a kijelzőn, méghozzá 440 Hz-en. Akkor most mi van? -kérdezi, hiszen az eddigi tanulmányok alapján a maszter buszon látható hullámforma felharmonikusokban gazdag spektrumeloszlást kéne hogy mutasson. Hát igen, itt jön be a lebegőpontos ábrázolás lényege. Hagyjunk most ki egy lépést ahhoz, hogy megértsük a dolgokat, és szimuláljuk a 24 bites fixpontos ábrázolást (mint ahogyan egy DA konverter előállítaná ezt a torzított szinuszt). Ehhez helyezzünk el az oszcilloszkóp után egy bitcsökkentő plugint, amit 24 bit fixpontra állítunk be (A dithert kapcsoljuk ki! lásd a mellékelt ábrán), és csak ez után helyezzük el a spektrumanalizátort. Vagyis most már a valódi 24 bites fixpontos spektrum képet fogjuk látni.
Meg is vannak a felharmonikusok, ahogy annak lennie kell. Aki egy kicsit szemfülesebb, már kapizsgálhatja, hogy mit is nyerhetünk a lebegőpontos ábrázolással és az általa nyújtott megnövekedett dinamikatartománnyal.
A példa alapján tehát azt gondolhatjuk, hogy a maszter buszon összegzett szinusz hullám már eltorzult, hiszen átlépte a 0 dBFS jelszintet, ami felett pedig nincsen semmi, ezért levágódnak a 0 dBFS fölé eső részek. Ez fixpontos ábrázolásnál igaz, lebegőpontos ábrázolásnál csak akkor, ha direkt ilyen funkciót állítunk be. A legtöbb DAW a csatornákon belüli számításokat lebegőpontosan végzi el, függetlenül attól, hogy milyen keverési bitmélységet állítottunk be. Ilyen pl. a Reaper is, bár most a keverést is lebegőpontosra kértük a projekt létrehozásakor (ez egyébként az alapbeállítás is, tehát külön nem kell kiválasztani). Mire jó mindez? Jöjjön akkor a csoda, amihez nem kell más, mint egy jelszint beállító plugin (vagy olyan, amin van ilyen jellegű poti). Az egyszerűség és a platformfüggetlenség miatt használjuk most az ingyenes MEqualizer-t, ami egy EQ plugin, de lehet vele halkítani és hangosítani is. Helyezzük el ezt az első insert pontra, vagyis az oszcilloszkóp plugin elé!
Kezdjük most csökkenteni az MEqualizerből kilépő, lebegőpontosan ábrázolt jelszintet az "OUTPUT" poti letekerésével. Hogy ne maradjunk le a csodáról, közben erősen figyeljük a maszter buszra elhelyezett oszcilloszkóp képét is! Mint láthatjuk, a jelszint csökkenésével kezd eltűnni a jelcsúcs vágása is, és ezzel együtt a kialakult felharmonikusok is. Ha elérjük a -6dB értéket, már az eredeti, torzítatlan szinusz hullámot kapjuk vissza, és a spektrumanalizátorok is azonos képet mutatnak. (Miért pont -6dB? Mert két 0 dBFS jel összege +6 dBFS, tehát ezt kell kompenzálni.) Vagyis bizonyítottuk, hogy a lebegőpontos ábrázolásnak köszönhetően a 0 dBFS feletti értékek nem vágódnak le (egészen +770 dBFS-ig), vagyis ha kompenzáljuk a létrejött túlvezérlést, nem történik adatvesztés mindaddig, amíg el nem hagyjuk a szoftver oldalt. Ha azt gondoljuk, hogy ez csak +6dB-ig működik, akkor bátran többszörözzük meg a bemenő jelet akár szintemeléssel, akár a sávok számának növelésével, majd kompenzáljunk a maszter busz bemenetén. Ehhez egy érték után már nem elegendő egyetlen jelszint csökkentő plugin, de annyit használhatunk, amennyit csak a DAW elbír, a jel minősége nem fog számottevően csökkenni.
Láthattuk tehát, hogy amíg a DAW-ban maradunk, addig a lebegőpontos ábrázolásnak köszönhetően nem okoz problémát a túlvezérlés. De mi történik akkor, amikor a DAW-ból kilép a jel? Hát nagyjából ugyanaz, mint amit az előbbi példákban egy szimulációval próbáltunk megjeleníteni. De hogy még szemléletesebb eredményt kapjunk, végezzünk el még egy kísérletet, ezúttal úgy, hogy a DAW kimenetét fájlokba mentjük.
Ehhez hozzunk létre egy 1000 Hz-es, 0 dBFS-re kivezérelt, 24 bites fixpontos ábrázolással WAV formátumba mentett szinusz hullámot, tetszőleges hosszban. (Az enyém pont 2 másodperces lett, mivel 120 BPM (ütem per perc) tempó mellett 1 zenei egész hosszban exportáltam.) A módszer nagyon egyszerű (szerintem már több részben is leírtam). Hozzunk létre egy új projektet a DAW-ban, és egy új sávot. Erre helyezzünk el egy hullámforma generátort (teszt hang generátor, tone generator, stb, pl. az ingyenes MOscillator), amin beállítjuk a fenti paramétereket. A legtöbb DAW-ban a plugin indítása és bekapcsolása után máris halljuk a hangot, ha nem így van, akkor lejátszáskor biztosan.
Jelöljük ki a szükséges időt, majd adjunk ki egy render utasítást (vagy export audio), ahol kimeneti formátumnak WAV 24 bit fixpontos monót adunk meg. Ha a sávunk eleve monó volt, akkor nagy valószínűséggel az exportált fájl is 0 dBFS jelszintű szinuszt fog tartalmazni, főként, ha a panoráma korrekció (pan law) is 0 dB-re volt állítva. Amelyik DAW-ban nincsen monó sáv (mint pl. REAPER), abban csak úgy kapunk 0 dBFS kimenetet, ha a pan law értéke 0 dB!
Ha nem megfelelő jelszintű fájlt kapunk, akkor az egyik lehetséges hibaforrás a monóban történő exportálás. Ha a DAW úgy exportál monóba, hogy a jobb és bal csatornát egyszerűen összeadja, akkor 0dBFS+0dBFS=+6dBFS jelszintet kapunk. Ilyen pl. a Cubase 9, ahol bár a fájlt visszatöltve 0 dBFS jelszintet látunk, a kapott szinusz csúcsai levágódnak, a hang torzított lesz (és erről semmilyen figyelmeztetést nem kapunk!). Itt megoldás lehet, ha a projekt panorámakorrekcióját -6dB-re állítjuk be, bár ezzel csak az exportált monó fájl megfelelő jelszintjét érjük el, mert a továbbiakban a DAW-ban rendre 6 dB-el alacsonyabb jelszinteket fogunk leolvasni. A Presonus Studio One 3.5-ben például nem lehet panoráma korrekciót állítani, az -3dB-re van gyárilag fixálva, így itt a 0 dBFS szinusz 3 dBFS jelszintet eredményezne, ha lehetne monóban exportálni, de nem lehet. Cserébe -3dBFS jelszintű sztereó fájlt kapunk. Mixbus 4 esetén szintén -3 dB a beépített panoráma korrekció, itt viszont monó exportálás esetén csatornát kell választani, vagyis nem a két oldal összegét, hanem valamelyik oldalt önmagában fogja lementeni. Ezekkel ellentétben a korrekt szoftverek, mint például a Reaper, úgy alakítják át a sztereó jelet monóvá, hogy az összeadás előtt a két oldal jelszintjét 6dB-el csökkentik. Ha lehetséges, válasszunk olyan opciót, ahol az elkészült fájlt azonnal vissza is tölti a DAW a projektbe, mert ezzel megspórolhatunk egy importálást.
Ha nem megfelelő jelszintű fájlt kapunk, akkor az egyik lehetséges hibaforrás a monóban történő exportálás. Ha a DAW úgy exportál monóba, hogy a jobb és bal csatornát egyszerűen összeadja, akkor 0dBFS+0dBFS=+6dBFS jelszintet kapunk. Ilyen pl. a Cubase 9, ahol bár a fájlt visszatöltve 0 dBFS jelszintet látunk, a kapott szinusz csúcsai levágódnak, a hang torzított lesz (és erről semmilyen figyelmeztetést nem kapunk!). Itt megoldás lehet, ha a projekt panorámakorrekcióját -6dB-re állítjuk be, bár ezzel csak az exportált monó fájl megfelelő jelszintjét érjük el, mert a továbbiakban a DAW-ban rendre 6 dB-el alacsonyabb jelszinteket fogunk leolvasni. A Presonus Studio One 3.5-ben például nem lehet panoráma korrekciót állítani, az -3dB-re van gyárilag fixálva, így itt a 0 dBFS szinusz 3 dBFS jelszintet eredményezne, ha lehetne monóban exportálni, de nem lehet. Cserébe -3dBFS jelszintű sztereó fájlt kapunk. Mixbus 4 esetén szintén -3 dB a beépített panoráma korrekció, itt viszont monó exportálás esetén csatornát kell választani, vagyis nem a két oldal összegét, hanem valamelyik oldalt önmagában fogja lementeni. Ezekkel ellentétben a korrekt szoftverek, mint például a Reaper, úgy alakítják át a sztereó jelet monóvá, hogy az összeadás előtt a két oldal jelszintjét 6dB-el csökkentik. Ha lehetséges, válasszunk olyan opciót, ahol az elkészült fájlt azonnal vissza is tölti a DAW a projektbe, mert ezzel megspórolhatunk egy importálást.
Ha mindent jól csináltunk, akkor most már 2 sávunk van a projektben. Az első az általunk létrehozott szinusz generátoros, a második az imént exportált WAV. Ha erre ráközelítünk, láthatjuk is a szinusz hullámot (legalábbis a jobb DAW-okban). Láthatjuk, hogy a hullám csúcsa nem vágódott le, és teljes egészében kitölti a rendelkezésére álló jelszintet, vagyis a képernyőn a függőleges irányt. Minderre azért volt szükség, hogy ne csak halljuk, hanem lássuk is, hogy mi történik a következő tesztben. A továbbiakban a generátor sávra már nincsen szükségünk, azt nyugodtan törölhetjük.
A fenti ábra felső részében vörösre színezett sávon láthatjuk a 0 dBFS kivezérlésű, fixpontosan ábrázolt szinuszhullámunkat. (Mivel 24 biten dolgozunk, de csak 0 dBFS-ig, így most a fixpontos ábrázolás semmivel sem rosszabb, mint a lebegőpontos.) Most duplikáljuk a sávot, ezzel létrehozva az ábra alsó részén látható narancs színű sávban található szinusz hullámot, ami most még pont ugyanolyan, mint az eredeti szinuszunk. A REAPER DAW-ban lehetőség van rá, hogy az egyes hangfájlok jelszintjét úgy változtassuk meg, hogy azt a DAW azonnal, grafikusan is megjeleníti. Ehhez -megfelelő beállítás mellett- elég a fájl neve előtt található mini potmétert elforgatnunk. A példa szerinti esetben -6dB-re csökkentettem a narancs hullám jelszintjét (ami valójában persze csak a mintaértékek osztását jelenti). A lényeg, hogy bár fixpontos ábrázolást használtunk, mivel 0 dBFS volt a wav fájl maximális jelszintje, a hullámforma nem vágódott le, és jelszintcsökkentéskor megtartja az eredetileg látható alakját. Vagyis itt a jel nem torzul.
Most állítsuk vissza a narancs szinusz jelszintjét 0-ra, majd némítsuk a sávot. Indítsuk el a lejátszást végtelenített módba kapcsolva, így egy 1000 Hz-es szinuszhullám tiszta hangját kell hogy halljuk, hiszen most csak 1 darab 0 dBFS jelszintű szinuszt hallunk. (Ha ezt exportálnánk, az eredeti szinuszhullámot kapnánk vissza.) Következő lépésként töröljük a második (narancs) sávról a némítást, és figyeljük meg, mi történik. Mivel most már 2 darab 0 dBFS jelszintű szinusz szól egyszerre, ezek jelszinte összeadódik, és mivel teljesen azonos a frekvenciájuk és a fázisuk is, így az eredő jelszint az eredeti duplájára nő, vagyis +6 dBFS-lesz (akárcsak az előző példában). Ezt olvashatjuk le a maszter busz kivezérlésmérőjén is, és hallhatjuk is a torzított szinusz hangját (de csak akkor, ha nincsen bekapcsolva a túlvezérlés biztosítás). Készítsünk erről az állapotról is egy rendert, pont ugyanúgy mint az előbb, vagyis 24 bit fixpontos, mono wav formában. (Figyeljünk rá, hogy a fájlnevet változtassuk meg, pl. "+6 dB szinusz 24 bit fixpont"-ra.) Ha megfigyeljük az automatikusan visszaimportált fájl képét, pontosan azt kapjuk, amiről az előző próbában szó volt. Ezt a következő ábrán sárga színű sávon találjuk. Mint látható, a szinusz csúcsai levágódtak, ami torzítást és felharmonikusokat idéz elő.
Nézzük, mi történik, ha most ezt a fixpontosan ábrázolt túlvezérelt fájlt halkítjuk le. Ehhez duplikáljuk a sárga sávot, majd a már ismertetett módon csökkentsük a jelszintjét 6dB-el. Mint az a létrehozott kék sávban látható, a hullámforma a fixpontos ábrázolás miatt a jelszint csökkentéskor megtartja az eredeti formáját. Bár a halkítás után a jelszintje -6dB-lesz, ami már nem jelez túlvezérlést a kivezérlésmérőn (lásd a kis piros jelölést, vagyis annak hiányát), a hangzás mégis torz marad, hiszen a levágott részek nem lettek a fájlba mentve. Ezeket a torzításokat normál esetben nem tudjuk visszaállítani, legalábbis nem egyszerű módon.
Tipp:
Léteznek bizonyos algoritmusok (audio declipper), amik egyfajta interpolációval és mesterséges intelligenciával megpróbálják kitalálni, hogy mi lehetett a levágott részeken, de gondolom az mindenki számára világos, hogy ott bármi lehetett, így a kitalációk jó esetben is csak megközelíthetik a valóságot, az eredeti hullámformát visszaállítani elméletileg lehetetlen. Jusson mindez eszünkbe, amikor figyelmen kívül hagyjuk a maszter sávon megjelenő túlvezérlésre figyelmeztető jelzést!
A hangkártya kimenetére pontosan ugyanaz a jel kerül, mint ami a DAW render (vagy export) által a fájlba. Legalábbis akkor, ha nem használunk úgynevezett monitor effekteket, amit nem csak Reaperben, de sok más DAW-ban, például Cubase-ben is megtalálhatunk. Ezek úgy módosítják a DAW-ból kilépő jelet, hogy az csak a monitorra van hatással, az exportált fájlokra nem. Ide érdemes elhelyezni pl. a monitor kalibrációt, vagy szobaakusztikai korrekciót.
Nézzük most, hogy mi a helyzet akkor, ha nem fixpontos, hanem lebegőpontos ábrázolást választunk a fájl elkészítéséhez! Ehhez némítsuk a sárga és kék sávokat (vagyis csak az eredeti két 0 dBFS szinusz szóljon egyszerre) és készítsünk egy lebegőpontos rendert. Ezt a legtöbb DAW-ban 32 bit FP (Floating point) néven találjuk meg (lásd a mellékelt ábrán). Ha elkészült a render, és be is importáltuk a kész fájlt, vessünk egy pillantást a hullámformára!
Első ránézésre pont ugyanazt kaptuk, mint amit a 24 bites fixpontos render esetén, vagyis a 32 bites lebegőpontos zöld és a 24 bites fixpontos sárga sáv teljesen azonos képet mutat, és nem mellesleg a hangjuk is pont ugyanolyan. Ne feledjük amit az előző részben már megtanultunk, hogy valójában ez is csak 24 bites audiót tartalmaz, de ezt a 24 bitet fel lehet nagyítani, vagy le lehet kicsinyíteni, attól függően, hogy 24 biten ábrázolható egész számoknál nagyobbat, vagy kisebbet akarunk-e tárolni. És akkor most kezdjük el a 32 bites lebegőpontos fájl jelszintjét csökkenteni, a már megismert módon. Csodák csodájára, itt a szinusz jel csúcsai nem maradnak levágva, az eredeti szinuszt tökéletesen vissza tudjuk állítani, ha megfelelő értékű kompenzációt alkalmazunk (esetünkben -6dB). Ha most összehasonlítjuk a -6dB-es 24 bites fixpontos (kék) és a -6dB-es 32 bites lebegőpontos (zöld) sáv hangját, rögtön halljuk, hogy az előbbi torzít, az utóbbi viszont teljesen tiszta szinuszt ad.
Tehát most már nem csak hanggal, hanem vizuálisan is bizonyítottuk, hogy lebegőpontos ábrázoláskor a 0 dBFS fölé eső jel nem vágódik le, nem veszik el, az megfelelő jelszintcsökkentéssel visszanyerhető. Ezt persze csak a lebegőpontos adatok fogadására és feldolgozására felkészített eszközök tudják megtenni, mint pl. egy DAW, vagy egy plugin. A fixpontos lejátszásra képes eszközök, mint például egy DA konverter, egy egyszerű CD vagy mp3 lejátszó nem képes erre.
Tehát most már nem csak hanggal, hanem vizuálisan is bizonyítottuk, hogy lebegőpontos ábrázoláskor a 0 dBFS fölé eső jel nem vágódik le, nem veszik el, az megfelelő jelszintcsökkentéssel visszanyerhető. Ezt persze csak a lebegőpontos adatok fogadására és feldolgozására felkészített eszközök tudják megtenni, mint pl. egy DAW, vagy egy plugin. A fixpontos lejátszásra képes eszközök, mint például egy DA konverter, egy egyszerű CD vagy mp3 lejátszó nem képes erre.
Ha tehát a munkánkat további feldolgozás céljából exportáljuk, például egy zenésztársunknak, vagy hangmérnöknek, esetleg maszteringre küldjük, akkor érdemes lebegőpontos formátumba exportálni, mert ilyenkor az esetleges túlvezérlés miatt nem következik be adatvesztés. (Legalábbis akkor, ha a túlvezérlést a címzett felismeri és csökkenti a fájl jelszintjét.) Tehát nem igaz az, hogy maszteringre úgy kell elküldeni a fájlt, hogy maradjon tartalék a 24 bit alatt. Ha lebegőpontosan küldjük a fájlt, akkor +770 dB-ig akár túlvezérlésbe is mehetünk a kimeneten, a masztering hangmérnök gyakorlatilag elhanyagolható veszteség árán vissza tudja húzni az anyagot a neki tetsző jelszintre.
Tipp:
Van egy nagyon is valós alapja annak, hogy miért kérnek a masztering hangmérnökök 24 bit fixpontos audiót. Az előző részben már említettük, hogy a 32 bites lebegőpontos hangfájlok szabványosítása még nem teljeskörű, a 24 biteseké viszont igen. Így a 24 bites fájlokkal nem lehet tévedni, a 32-vel viszont lehetnek problémák. Arra pedig, hogy miért kérnek -10 dB csúcsértékre kivezérelt fájlokat az a magyarázat, hogy ezzel próbálják elkerülni a gyors tranziensek által előidézett túlvezérléseket a 24 bites fixpontos fájlokban.
Mit állapíthattunk meg mindebből? Fixpontos ábrázolás esetében 0 dBFS-ig nem jön létre torzítás (legalábbis nem túlvezérlés következtében), sem a sávokon, sem a buszokon, vagy a maszter buszon. Lebegőpontos ábrázolás esetén +750 dBFS-ig sem a sávokon, sem a buszokon, sem a maszter buszon nem jön létre visszaállíthatatlan torzítás, ha túlvezérlés keletkezik. Erre azonban a DAW kivezérlésmérők minden esetben figyelmeztetnek. Ilyenkor nincsen más dolgunk, csak csökkenteni a jelszintet (vagy jelszinteket) mindaddig, amíg az 0 dBFS alá nem csökken. Ha ezt nem tesszük meg, akkor fixpontos ábrázolás esetén (például régi pluginek, vagy exportálás) a túlvezérlésből eredő jelcsúcsvágások nem visszafordíthatóak. Ha viszont lebegőpontos ábrázolást használunk, akkor megfelelő jelszintcsökkentéssel az eredeti hullámforma gyakorlatilag mindig visszaállítható.Tehát kijelenthetjük, hogy ha erre felkészített szoftvereket használunk, akkor a túlvezérlésmérőkön jelzett túlvezérlés nem jelent minőségcsökkenést, sem pedig adatvesztést mindaddig, amíg a jelszint ábrázolható a rendelkezésre álló lebegőpontos biteken, és a digitális tartományon belül maradunk (lebegőpontos adattovábbítás és feldolgozás). Szintén nem történik jelentős torzítás, amennyiben a DAW elhagyása előtt (DA konverter vagy fixbites render) a jelszintet csökkentjük a szükséges értékre (24 vagy 16 bit fixpontos ábrázolás). A megfelelő kompenzációs érték (jelszintcsökkentés) megtalálásában segít a maszter busz túlvezérlésjelzője!
Analóg modellezett pluginek
Túlvezérlésjelző lebegőpontos ábrázolás esetén
Mivel a konverterek "csak" fixpontos ábrázolással képesek működni, így nem képesek a lebegőpontos értékekkel mit kezdeni. A szoftver hiába tud 0 dBFS fölé menni, ha a hardver ezt nem képes megszólaltatni. Vagyis ilyen esetben mindenképpen adatvesztés történik. Tehát nagyon helyesen a DAW (és általában a pluginek) kivezérlésmérője 0 dBFS jelszint elérésekor, vagy felette jeleznek túlvezérlést, függetlenül attól, hogy lebegőpontos, vagy fixpontos működést végeznek-e
Természetesen lebegőpontos működés esetén a 0 dBFS feletti jelszinteken lévő adatok nem vesznek el a szoftver oldalon, de ha figyelembe vesszük, hogy a technika mai állása szerint 24 bit felbontásnál nagyobb digitalizálásnak nincsen értelme, máris érthetővé válik, hogy a DAW kivezérlésmérője 32 vagy 64 bit lebegőpontos beállítás esetén is 24 bit fixponthoz "próbál igazodni" (8 vagy 16 bitet gyakorlatilag már senki sem használ). Ez azt jelenti, hogy a 24 bit fixpontos ábrázolással felírható értékeket helyezi előtérbe, mondhatjuk úgy is, hogy a digitál-analóg konvertereket tartja szem előtt. (Nem mellesleg a "mantissza" is 24 bites, 23 bit+1 bit előjel, akárcsak a 24 bites fixpontos ábrázolás.)
Tehát ha egy sávon (vagy pluginben) megjelenik a túlvezérlést jelző vörös fény, akkor az azt jelenti, hogy az adott sávot már nem lehet a 24 bites fixpontos konverteren információveszteség nélkül megszólaltatni. Persze a modern DAW-okban, ha csak a maszter kimenet kerül DA átalakításra, akkor az egyes sávokon nem jelent problémát a túlvezérlés (ettől még kerülni kell), hiszen a 32 bit lebegőpontos adattovábbításnak köszönhetően a DAW-on belül -kb. 1500 dB dinamikatartományig- nem történik információvesztés. Ha viszont a maszter kimeneten látjuk a túlvezérlést, akkor biztosak lehetünk benne, hogy ez a 24 bites konverteren már információveszteséget jelent majd.
32 bit lebegőpont konvertálása 24 bit fixpontra
Mivel a konverterek csak fixpontosan képesek működni, ezért a DA átalakítás előtt a konverter meghajtóprogramjába érkező jelet 24 vagy 16 bit fixpontossá kell alakítani. Hogy ez hogyan történik meg, azt a gyártó tudja csak megmondani. Viszont jó ha tudjuk, hogy ha 24 bites fixpontos adatot küldünk ki a DAW-ból, az már biztosan nem lesz újra konvertálva. Ez nekünk azért jó, mert így biztosak lehetünk benne, hogy a 32 bit lebegőpontos - 24 bit fixpontos átalakítás pont úgy történik meg, ahogyan azt mi szeretnénk. Vagyis mi határozhatjuk meg a végső hangzást. (16 bites kimenet esetében még inkább hallhatóak a különbségek.)
Mivel a bitszám csökkentés minden esetben kvantálási zaj hozzáadásához és torzításhoz vezet, ezért az átalakítás során érdemes Dither-t alkalmazni. Ezzel elkerülhető, hogy túl sok adatot veszítsünk a halk részeken, amitől egyébként a mixünk szűkebb, kevésbé térhatású és zajosabb hangzású lenne.
Mivel a konverterek "csak" fixpontos ábrázolással képesek működni, így nem képesek a lebegőpontos értékekkel mit kezdeni. A szoftver hiába tud 0 dBFS fölé menni, ha a hardver ezt nem képes megszólaltatni. Vagyis ilyen esetben mindenképpen adatvesztés történik. Tehát nagyon helyesen a DAW (és általában a pluginek) kivezérlésmérője 0 dBFS jelszint elérésekor, vagy felette jeleznek túlvezérlést, függetlenül attól, hogy lebegőpontos, vagy fixpontos működést végeznek-e
Természetesen lebegőpontos működés esetén a 0 dBFS feletti jelszinteken lévő adatok nem vesznek el a szoftver oldalon, de ha figyelembe vesszük, hogy a technika mai állása szerint 24 bit felbontásnál nagyobb digitalizálásnak nincsen értelme, máris érthetővé válik, hogy a DAW kivezérlésmérője 32 vagy 64 bit lebegőpontos beállítás esetén is 24 bit fixponthoz "próbál igazodni" (8 vagy 16 bitet gyakorlatilag már senki sem használ). Ez azt jelenti, hogy a 24 bit fixpontos ábrázolással felírható értékeket helyezi előtérbe, mondhatjuk úgy is, hogy a digitál-analóg konvertereket tartja szem előtt. (Nem mellesleg a "mantissza" is 24 bites, 23 bit+1 bit előjel, akárcsak a 24 bites fixpontos ábrázolás.)Tehát ha egy sávon (vagy pluginben) megjelenik a túlvezérlést jelző vörös fény, akkor az azt jelenti, hogy az adott sávot már nem lehet a 24 bites fixpontos konverteren információveszteség nélkül megszólaltatni. Persze a modern DAW-okban, ha csak a maszter kimenet kerül DA átalakításra, akkor az egyes sávokon nem jelent problémát a túlvezérlés (ettől még kerülni kell), hiszen a 32 bit lebegőpontos adattovábbításnak köszönhetően a DAW-on belül -kb. 1500 dB dinamikatartományig- nem történik információvesztés. Ha viszont a maszter kimeneten látjuk a túlvezérlést, akkor biztosak lehetünk benne, hogy ez a 24 bites konverteren már információveszteséget jelent majd.
32 bit lebegőpont konvertálása 24 bit fixpontra
Mivel a konverterek csak fixpontosan képesek működni, ezért a DA átalakítás előtt a konverter meghajtóprogramjába érkező jelet 24 vagy 16 bit fixpontossá kell alakítani. Hogy ez hogyan történik meg, azt a gyártó tudja csak megmondani. Viszont jó ha tudjuk, hogy ha 24 bites fixpontos adatot küldünk ki a DAW-ból, az már biztosan nem lesz újra konvertálva. Ez nekünk azért jó, mert így biztosak lehetünk benne, hogy a 32 bit lebegőpontos - 24 bit fixpontos átalakítás pont úgy történik meg, ahogyan azt mi szeretnénk. Vagyis mi határozhatjuk meg a végső hangzást. (16 bites kimenet esetében még inkább hallhatóak a különbségek.)
A sorozat következő részében a Dither sötét bugyraiba merülünk majd le, és talán meglátjuk a kivezető alagútban lévő fényt is.
Addig is eredményes keverést kívánok mindenkinek!
A következő részhez katt ide...
Felhasznált irodalom:
http://sound.whsites.net/noise.htm
http://mti.kvk.uni-obuda.hu/adat/tananyag/passziv/Passziv8Zajok2014.pdf
https://en.wikipedia.org/wiki/Signedness
http://nwavguy.blogspot.com/2011/09/noise-dynamic-range.html
https://www.researchgate.net/publication/324822062_Measurement_of_Sound_Pressure_Levels_in_Anechoic_Chamber_and_a_Noisy_Environment_Experimentally
https://www.soundonsound.com/techniques/digital-problems-practical-solutions
https://en.wikipedia.org/wiki/Line_level
https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch4.pdf
http://www.digitalfishphones.com/main.php?item=2&subItem=6
https://en.wikipedia.org/wiki/Denormal_number
https://en.wikipedia.org/wiki/IEEE_754
https://www.sounddevices.com/32-bit-float-files-explained/
https://www.discovermagazine.com/environment/the-loudest-sound-ever-heard
Nincsenek megjegyzések:
Megjegyzés küldése